Théorème de Desargues
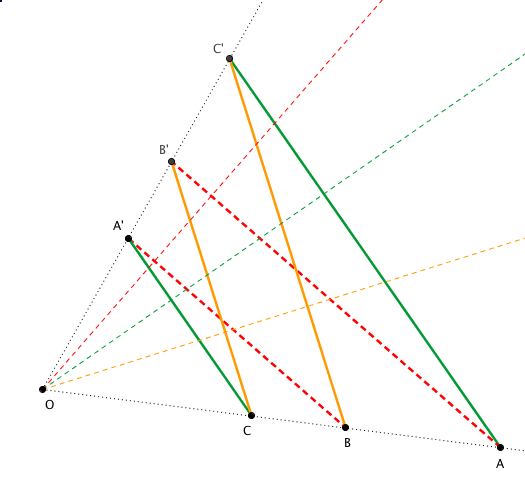 |
notationsa = |O A| b = |O B| c = |O C| a' = |O A'| b' = |O B'| c = |O C'| |
Notations

P étant le projeté orthogonal de A sur O P
la = |O A| et lp = |O P|
θ étant l'angle A O P
la relation entre les longueurs la et lp est noté :
θ la = lp (plus traditionellement : la cos(θ) = lp)
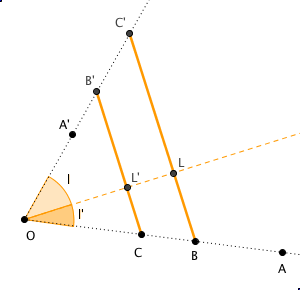 |
soit L le projeté orthogonal de O sur B C'
soit L' le projeté orthogonal de O sur C B'
soit l l'angle C' O L = B' O L'
soit l' l'angle C O L' = B O L
l'b = lc' (1)
l'c = lb' (2)
|
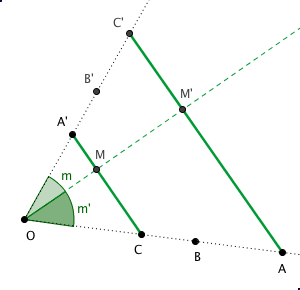 |
soit M le projeté orthogonal de O sur C A'
soit M' le projeté orthogonal de O sur A C'
soit m l'angle A' O M = C' O M'
soit m' l'angle C O M = A O M'
m'a = mc' (3)
m'c = ma' (4)
|
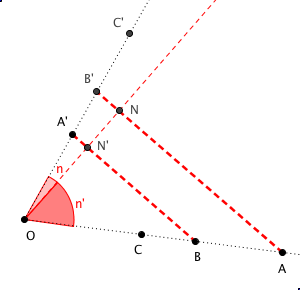 |
soit N le projeté orthogonal de O sur A B'
soit N' l l'intersection de O N et A' B
soit n l'angle B' O N = A' O N'
soit n' l'angle B O N' = A O N
nb' = n'a (5)
il faut prouver que na'=n'b (6)
|
|
l'b = lc' (1)
l'c = lb' (2)
m'a = mc' (3)
m'c = ma' (4)
nb' = n'a (5)
na'=n'b ? (6)
|
démonstrationl' n' b = n' l' b (l13_7)
l' n' b = n' l c' (1)
m l' n' b = m n' l c'
= n' m l c' = n' l m c' (l13_7)
= n' l m' a (3)
= l m' n' a (l13_7)
= l m' n b' (5)
= m' n l b' (l13_7)
= m' n l' c (2)
= n l' m' c (l13_7)
= n l' m a' (4)
= m l' n a' (l13_7)
on a donc m l' n' b = m l' n a'
d'où n' b = n a'
CQFD |