Théorème de Desargues
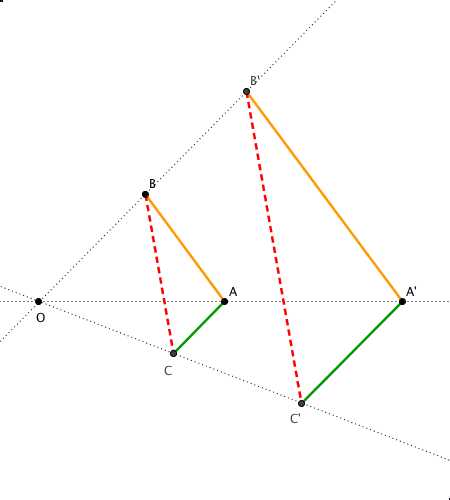
O B || A C
A B |.| A' B'
A C |.| A' C'
démonstration
supposons que B C et B' C' ne sont pas parallèles
alors soit B C n'est pas parallèle à O A,
soit B' C' n'est pas parallèle à O A
soit B' C' n'est pas parallèle à O A
supposons que B C n'est pas parallèle à O A
on construit d la parallèle à B C passant par B'
puisque B C intercepte O C (en C)
et d || B C, d intercepte O C (l12_6)
et d || B C, d intercepte O C (l12_6)
soit C'' l'intersection de d et O C, (C'' ≠ C')
d'après Desargues (démonstration 1),
B C || B' C'' et A B || A' B'
=>A C || A' C''
B C || B' C'' et A B || A' B'
=>A C || A' C''
on est bien dans le cas de la démonstration 1 puisque par hypothèse ¬ B C || O A
comme A C || A' C' et A C || A' C''
on en déduit A' C' || A' C''
on en déduit A' C' || A' C''
donc les droites A' C' et A' C'' sont confondues, on en déduit que C'' ∈ A' C'
puisque C'' ∈ O C et C'' ∈ A' C'
C'' ∈ O C ∩ A' C'
C'' ∈ O C ∩ A' C'
comme C' ∈ O C ∩ A' C', en raison de l'unicité du point d'intersection de deux droites, on en déduit C' = C'',
ce qui contredit l'hypothèse
donc B C || B' C'
dans le cas où B C || O A :
puisque ¬ B C || B' C' on a ¬ B' C' || O A
un raisonnement identique en permutant les rôles de B C et B' C' aboutit à la même conclusion
puisque ¬ B C || B' C' on a ¬ B' C' || O A
un raisonnement identique en permutant les rôles de B C et B' C' aboutit à la même conclusion
CQFD