Théorème de Desargues
En définissant :
A B || PC D :=
∃ X Y, Col P X Y /\ A B ⊥ X Y /\ C D ⊥ X Y
il existe une perpendiculaire commune à A B et C D passant par P
A B || PC D <=> A B || C D
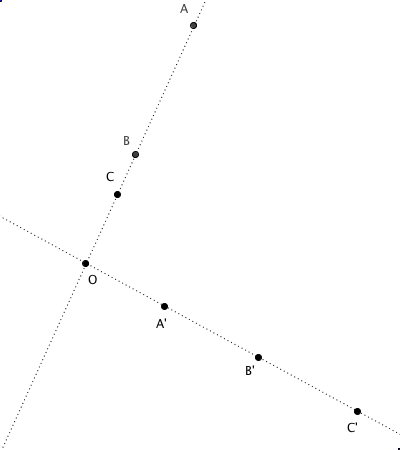 |
 |
∀ O A B C A' B' C',
¬ Col O A A'
Col O A B /\ Col O B C /\ B ≠ O /\ C ≠ O
Col O A' B' /\ Col O B' C' /\ B' ≠ O /\ C' ≠ O
A C' || O C A'
B C' || O C B'
=> A B' || O B A'
Col O A B /\ Col O B C /\ B ≠ O /\ C ≠ O
Col O A' B' /\ Col O B' C' /\ B' ≠ O /\ C' ≠ O
A C' || O C A'
B C' || O C B'
=> A B' || O B A'