On se place dans le cas non dégénéré où : /ABCD/ et /CDEF/ sont des parallélogrammes stricts
Il en découle que :
A ≠ B , A ≠ C , A ≠ D , B ≠ C , B ≠ D , C ≠ D et C ≠ E , C ≠ F , D ≠ E , D ≠ F , E ≠ F
Pseudo-transitivité des parallélogrammes
∀ A B C D E F, /ABCD/ → /CDEF/ → /ABFE/
Utiliser la barre d'espace pour progresser
Définition du parallélogramme
Parallelogram A B C D := Parallelogram_strict A B C D \/ Parallelogram_flat A B C D
Définition du parallélogramme strict
Parallelogram_strict A B C D :=
two_sides AC BD /\ AB // CD /\ AB ≡ CD
Définition du parallélogramme plat
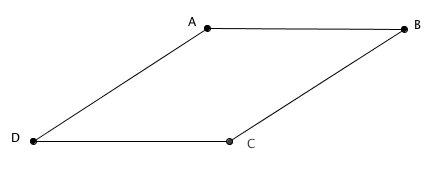
Parallelogram_flat A B C D :=
Col A B A' /\ Col A B B' /\ AB ≡ CD /\ AD ≡ BC /\ (A ≠ C \/ B ≠ D)
Cas particulier : A = E
/ABCD/ → /CDAF/ → /ABFA/
/CDAB/ → /CDAF/ → /ABFA/ (symmétrie)
Etant donnés 3 points, il existe un unique quatrième point formant un parallélogramme avec les trois autres points, donc B = F
/CDAB/ → /CDAF/ → /ABFA/
/CDAB/ → /CDAB/ → /ABBA/ (parallélogramme trivial)
Cas général : A ≠ E
On prolonge DC par D' de sorte que DC ≡ CD'
puisque D ≠ C on a C ≠ D'
sachant que DC // AB, on a A et B situés du même coté de CD
en utilisant le théorème "par_preserves_conga_os" : deux parallèles coupent une droite selon le même angle :
DA // BC → Bet D C D' → C ≠ D' → one_side DC AB → ADD' ≡ BCD'
on en déduit que ADD' ≡ BCD'
de même, sachant que CD // EF on a E et F situés du même coté de CD
on en déduit que EDD' ≡ FCD'
On en déduit que ADE ≡ BCF
Il faut cependant distinguer deux cas selon que A et E sont situés de part et d'autre de CD ou du même coté de CD
Dans le premier cas on utilise le théorème "l11_22a" et dans le second cas le théorème "l11_22b"
l11_22a A D E D' B C F D' :
two_sides DD' AE /\ two_sides CD' BF
/\ ADD' ≡ BCD' /\ D'DE ≡ D'CF
→ ADE ≡ BCF
l11_22b A D E D' B C F D' :
one_side DD' AE /\ one_side CD' BF
/\ ADD' ≡ BCD' /\ D'DE ≡ D'CF
→ ADE ≡ BCF
Puisque /ABCD/ et /CDEF/ on a :
AD ≡ BC et DE ≡ CF
comme ADE ≡ BCF les triangles sont identiques
donc DAE ≡ CBF , DEA ≡ CFB et AE ≡ BF
Cas 1 : A E F alignés
On doit alors prouver que /ABFE/ est un parallélogramme dégénéré (plat)
ou par symmétrie que /FEAB/ est un parallélogramme plat.
Il faut donc prouver :
- Col F E A /\ Col F E B (1)
- FE ≡ AB (2)
- FB ≡ AE (3)
- (F ≠ A \/ E ≠ B) (4)
- Puisque AEF alignés et AB // EF on a ABEF alignés ce qui prouve (1)
- Puisque /ABCD/ et /CDEF/ on a AB ≡ CD et CD ≡ EF et par transitivité de la congruence AB ≡ EF (2)
- FB ≡ AE a été déduit du fait que ADE et BCF sont des triangles identiques (3)
- Si on suppose A = F et B = E alors l'hypothèse : CF // DE (car /CDEF/) devient CA // DB, or comme CA et DB sont les diagonales de /ABCD/ elles se coupent en leur milieu et ne sont donc pas parallles. On en déduit donc que F ≠ A \/ E ≠ B (4)
Ainsi lorsque A B E sont alignés , ABFE est bien un parallélogramme plat, donc un parallélogramme.
Cas 2 : A E F non alignés
Le théorème "pars_par_plg" affirme que si AB // EF et AE // BF alors /ABFE/
pars_par_plg : ∀ A B C D , Par_strict A B C D → Par A D B C → Parallelogramm A B C D
Puisque AB // FE (transitivité), pour prouver /ABFE/ il suffit de montrer que AE // BF
Il suffirait de montrer si deux triangles ABC et A'B'C' sont identiques, si AB // A'B' et BC // B'C' alors AC // A'C'
Cette assertion qui à première vue semble vraie est malheureusement fausse
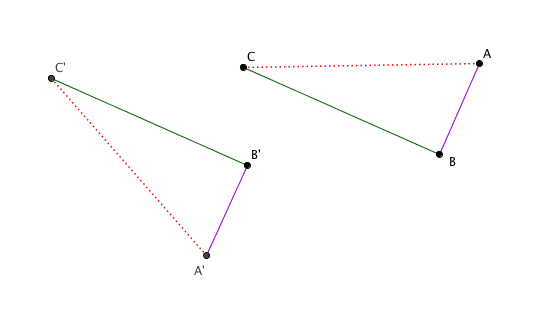
Cependant notre construction impose :
- AA' //s BB'
- CC' //s BB'
or dans le cas cité en contre-exemple l'une des propriétés ci-dessus est fausse
AA' //s BB' est faux
nous allons donc montrer que :
- si deux triangles sont identiques alors
- AB // A'B'
- CB // C'B'
alors AC // A'C' ou AA' //s BB' ou CC' //s BB'
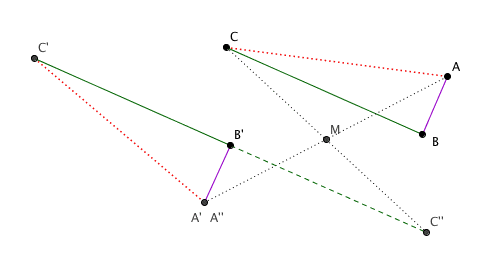
On construit M le milieu de BB' dont l'existence est assurée par le théorème "midpoint_existence"
Puis on construit A'' le symmétrique de A par rapport à M et C'' celui de C
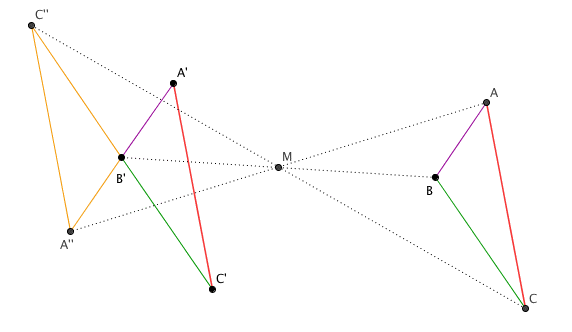
Par construction AB A''B' est un parallélogramme donc AB // A''B' (p1)
Par construction CB C''B est un parallélogramme donc CB // C''B' (p2)
Par construction AC A''C'' est un parallélogramme donc AC // A''C'' (p3)
Comme par hypothèse on a AB // A'B' et CB // C'B', on obtient par transitivité
- A'B' // A''B' (p4) → A'B'A'' alignés (1)
- C'B' // C''B' (p5) → C'B'C'' alignés (2)
La symétrie préservant les distances, on a : AB ≡ A''B' et CB ≡ C''B'
Par hypothèse les deux triangles sont identiques, donc : AB ≡ A'B' et CB ≡ C'B'
Par transitivité de la congruence on obtient :
- A'B' ≡ A''B' (3)
- C'B' ≡ C''B' (4)
puisque
A'B'A'' sont alignés (1) et A'B' ≡ A''B' (3)
C'B'C'' sont alignés (2) et C'B' ≡ C''B' (4)
D'après le théorme l7_20 :
∀ M A B , Col A M B → MA ≡ MB → A = B \/ is_midpoint M A B
on a :
- A' = A'' \/ B' est le milieu de A'A''
- C' = C'' \/ B' est le milieu de C'C''
a
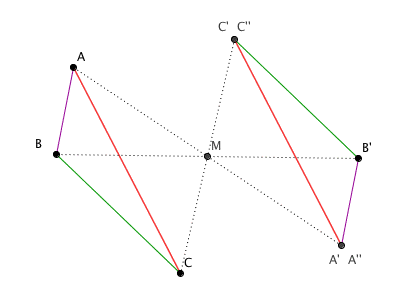
On doit donc distinguer 4 cas :
- A' = A'' et C' = C''
- B' est le milieu de A'A'' et B' est le milieu de C'C''
- A' = A'' et B' est le milieu de C'C''
- C' = C'' et B' est le milieu de A'A''
b
c
Cas a : A' = A'' et C' = C''
Puisque :
- AC // A''C'' (p3)
- A' = A'' et C' = C''
par substitution on obtient immédiatement AC // A'C' (cqfd)
Cas b : B' est le milieu de A'A'' et B' est le milieu de C'C''
Puisque : B' est le milieu de A'A'' et B' est le milieu de C'C'',
A'C'A''C'' est un parallélogramme
donc A'C' // A''C''
puisque AC // A''C'' (p3) , par transitivité du parallélisme on obtient AC // A'C' (cqfd)
Cas c : A' = A'' et B' est le milieu de C'C''
Cas particulier : A B C alignés
Si A B C sont alignés alors A'B'C' sont alignés
l4_13 : ∀ A B C A' B' C' , Col A B C → Cong_3 A B C A' B' C' → Col A' B' C'
comme
- ABC alignés → AB // AC
- A'B'C' alignés → A'B' // A'C'
puisque :
- AB // A'B' (hypothèse)
- AB // AC
- A'B' // A'C'
Par transitivité du parallélisme on a AC // A'C' (cqfd)
Cas c : A' = A'' et B' est le milieu de C'C''
Cas général : A B C non alignés
Si A B C sont alignés alors A'B'C' sont alignés
si A B C non alignés :
- M milieu de BB' (par construction)
- M milieu de A A'' (par construction) donc M milieu de AA' (car A' = A'')
on a BB' //s AA' (cqfd)
Cas d : C' = C'' et B' est le milieu de A'A''
identique au cas c) en permutant les rôles de A et C et ceux de A' et C'